A relação entre arte e matemática é mais antiga do que imaginamos.
Vamos fazer uma pequena viagem pela história da arte, desde as culturas pré-colombianas até à arte contemporânea com alguns exemplos.
Texto de Rute Ferreira, autora de cursos online na área de Análise de Arte e Museologia.
Gostas de matemática? Bem, muitos de nós tivemos problemas com a matemática nos tempos de escola (eu sei que tinha muitos!) e por isso nos cansámos da mesma.
Por isso, quando comecei a estudar história de arte, fiquei surpreendida ao perceber quão intimamente arte e matemática estão ligadas.
Tens dúvidas? Então, fica comigo enquanto revelo um pouco desta relação fascinante.
As relações entre arte e matemática são mais antigas do que pensamos…
Nas culturas pré-colombianas, por exemplo, há uma infinidade de obras de arte (na verdade, artefactos estéticos) que demonstram o conhecimento de padrões geométricos.
Ainda assim estas relações tornaram-se, de facto, mais aparentes durante o Renascimento.
Quando os artistas perceberam que noções básicas de matemática, como a perspectiva ou a simetria, tornariam as obras mais realistas.
o Homem de Vitrúvio
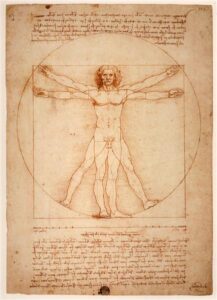
Leonardo da Vinci, o Homem de Vitrúvio, 1490, Gallerie dell’Accademia
Um dos trabalhos mais significativos nesse sentido foi, na verdade, um estudo.
Em 1490, Leonardo da Vinci expõe em papel o conceito de proporção concebido por Vitrúvio, um
arquitecto romano do primeiro século da nossa era.
Neste esboço, que é uma das obras mais aclamadas de Da Vinci, o artista usou a matemática para elaborar as proporções ideais do corpo humano.
De acordo com os cálculos, a medida do comprimento dos braços abertos de um homem é igual à sua altura, por exemplo.
Leonardo desenhou, detalhadamente, o homem, conhecido por nós como homem de Vitrúvio, e posicionou-o em duas formas geométricas bem conhecidas:
Um círculo e um quadrado, uma composição que se tornou digna de nota, considerando a organização do desenho.
a proporção áurea
E já ouviste falar da proporção áurea? Também conhecida como proporção de ouro ou Proporção Divina.
Esta é uma constante real irracional de álgebra que tem o valor aproximado de 1,618.
Esta constante (como o nome indica, algo fixo, uma oposição ao conceito de variável) é representada pela letra grega φ (Phi).
É uma homenagem a um artista: o escultor Phidias, que usou esta proporção para projectar uma das obras arquitectónicas mais notáveis da Antiguidade: o Partenon.
Leia o artigo: Porque é que no Partenon não é possível encontrar linhas retas?
a proporção áurea na Mona Lisa
Mona Lisa, Leonardo da Vinci, 1503, Musée du Louvre
A proporção de ouro é um padrão que se repete na natureza.
É por isso que é tão fascinante e tão celebrado por muitos artistas renascentistas que queriam recuperar os ideais da Antiguidade, mas, ao mesmo tempo, fundamentar a sua arte em evidências científicas.
A Mona Lisa, outra obra-prima de Leonardo da Vinci, apresenta a proporção de ouro no rosto, bem como na relação pescoço-cabeça, o que significa que o rácio entre as duas partes é de 1,618.
Isto deve-se ao interesse de Da Vinci não apenas em anatomia, mas também em matemática.
Porém, as relações entre arte e matemática não foram apenas evidentes no período do Renascimento.
A Arte Moderna foi um campo fértil para obras que estavam de alguma forma ligadas ao cálculo como veremos a seguir.
arte e matemática nas obras de Wassily Kandinsky
Wassily Kandinsky, Composition 8, 1923, Guggenheim Museum
O artista russo Wassily Kandinsky, conhecido pelas suas obras de arte abstratas e por ser professor na Bauhaus, foi um dos pintores que utilizou a matemática nas suas criações.
Nos seus trabalhos mais abstratos, Kandinsky usou muitos conceitos matemáticos. Círculos concêntricos, linhas abertas e fechadas, triângulos.
A geometria, em particular, foi um elemento de interesse do artista.
Isto não foi surpreendente, considerando que a Bauhaus procurava precisamente ser uma escola de arte e arquitetura que ampliava a ideia de arte e evidenciava as suas inúmeras possibilidades.
O interesse de Kandinsky por elementos matemáticos faz assim todo o sentido e o estabelecimento de relação entre arte e matemática também.
Piet Mondrian e o Neoplasticismo
Piet Mondrian, Composition with Red, Blue and Yellow, 1930, Private Collection.
Mas Kandinsky não era o único interessado na abstração geométrica enquanto possibilidade artística e na relação entre a arte e matemática .
Por volta de 1930, o artista Piet Mondrian produziu algumas composições que deram origem ao
Enquanto explorava a origem do Neoplasticismo, Mondrian usou conceitos matemáticos para chegar à conclusão:
“Concluí que o ângulo reto é a única relação invariável e que, pelas proporções da dimensão, podemos dar movimento à sua expressão constante, ou seja, fazendo-o consegui excluir cada vez mais das minhas pinturas as linhas curvas, até que finalmente as minhas composições consistiam apenas de linhas horizontais e verticais que formavam intersecções, cada uma separada e independente das outras (…).
Comecei a determinar formas: rectângulos verticais e horizontais, como todas as formas, tentam prevalecer uns sobre os outros e devem ser neutralizados pela composição.
Por fim, os rectângulos nunca são um fim em si mesmos, são uma consequência lógica das linhas que os definem, que são contínuas no espaço, e aparecem espontaneamente quando as interseções são dadas por linhas verticais e horizontais.
Os rectângulos suprimem a manifestação dos planos espaciais enquanto reduzem a cor e acentuam as linhas que os definem.”
Conheça este movimento artístico no vídeo seguinte.
Jackson Pollock
Jackson Pollock, Number 1, 1948, MoMA
Também o pintor americano Jackson Pollock, um dos pintores mais conhecidos do expressionismo abstracto e um dos artistas modernos mais controversos, interligou arte e matemática.
Na década de 90, o físico americano Richard Taylor, da Universidade de Oregon, observou nas pinturas de Pollock uma relação com o modelo geométrico de fractais.
Os fractais são, por definição, figuras de geometria não euclidiana e, geralmente, designam uma estrutura geométrica complexa cujas propriedades são repetidas em qualquer escala.
Mas como estão os fractais ligados à obra de Pollock?
Pollock utilizou nas suas pinturas uma técnica de dripping (salpicar) que faz com que o seu trabalho pareça aleatório.
Mas, aparentemente, não poderíamos estar mais errados.
Taylor dividiu as obras em quadrados de vários tamanhos, desde 1 centímetro a quase 5 metros, o que demonstrou que, na verdade, o padrão geométrico se repete.
Além disso, enquanto media a dimensão fractal dos trabalhos, Taylor observou que quanto mais Pollock desenvolvia esta técnica, maiores eram os valores.
Enfim, eu poderia continuar a escrever exemplos de “cortejo” entre arte e matemática indefinidamente, porque de alguma forma eles acabam sempre por se encontrar.
Espero apenas que se, como eu, tiveste problemas com a matemática no passado, consigas ser agora um pouco mais amigável com os cálculos daqui para a frente.
Aprenda mais sobre análise de arte nos cursos online
Rute Ferreira
Sou professora de Arte, com formação em Teatro, História da Arte e Museologia. Também sou especialista em Educação à Distância e atuo na educação básica. Escrevo regularmente no blog do Citaliarestauro.com e na Dailyartmagazine.com. Acredito firmemente que a história da arte é a verdadeira história da humanidade.
2 Comentários.
Muito interesante seu trabalho de pesquisa …continue assim!!!
Parabéns!!!
Gostei do trabalho, apesar de iniciante vejo no seu trabalho uma boa fonte de conhecimento.